Answer:
1. sin(Z) = 0.6
2. sin(C) = 0.28
3. cos(Z) = 0.8
4. tan(C) = 0.75
5. tan(50°) = 1.1918
6. cos(40°) = 0.7660
7. sin (25°) = 0.4226
8. sin(75°) = 0.9659.
Explanation:
The trigonometric ratios are
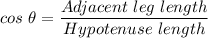
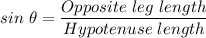
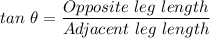
1. The length of the opposite leg to angle Z = 24
The length of the hypotenuse side = 40
∴ sin(Z) = 24/40 = 0.6
2. The length of the opposite leg to angle C = 14
The length of the hypotenuse side = 50
∴ sin(C) = 14/50 = 0.28
3. The length of the adjacent leg to angle Z = 24
The length of the hypotenuse side = 30
∴ cos(Z) = 24/30 = 0.8
4. The length of the opposite leg to angle C = 27
The length of the adjacent leg = 36
∴ tan(C) = 27/36 = 0.75
5. Using the calculator, and rounding the answers to the nearest 10,000, we have;
tan(50°) = 1.1918
6. Using the calculator, and rounding the answers to the nearest 10,000, we have;
cos(40°) = 0.7660
7. Using the calculator, and rounding the answers to the nearest 10,000, we have;
sin (25°) = 0.4226
8. Using the calculator, and rounding the answers to the nearest 10,000, we have;
sin(75°) = 0.9659.