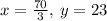Question

Find the solution to the following system of equations. x-2/3y=8 -1/5x+1/3y = 3

Answer 1

Note: Your question sounds a little unclear, but I am assuming that your system of equations is:

`x-(2)/(3)y=8`

`-(1)/(5)x+(1)/(3)y\:=\:3`

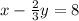
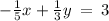
It would anyways clear your concept because the procedure to find the solutions remains the same for any set of a system of equations.

Answer:

The solution of the system of equations be:

`x=(70)/(3),\:y=23`

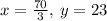
Explanation:

Given the system of equations

`\begin{bmatrix}x-(2)/(3)y=8\\ -(1)/(5)x+(1)/(3)y=3\end{bmatrix}`

`\mathrm{Multiply\:}-(1)/(5)x+(1)/(3)y=3\mathrm{\:by\:}5\:\mathrm{:}\:\quad \:-x+(5)/(3)y=15`

`\begin{bmatrix}x-(2)/(3)y=8\\ -x+(5)/(3)y=15\end{bmatrix}`

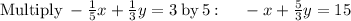
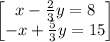
so adding the equation

`-x+(5)/(3)y=15`

`+`

`\underline{x-(2)/(3)y=8}`

`y=23`

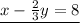
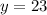
so the system equations become

`\begin{bmatrix}x-(2)/(3)y=8\\ y=23\end{bmatrix}`

`\mathrm{For\:}x-(2)/(3)y=8\mathrm{\:plug\:in\:}y=23`

`x-(2)/(3)\cdot \:23=8`

`x-(46)/(3)=8`

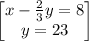
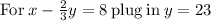
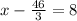
Add 46/3 to both sides

`x-(46)/(3)+(46)/(3)=8+(46)/(3)`

`x=(70)/(3)`

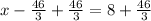
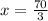
Therefore, the solution of the system of equations be:

`x=(70)/(3),\:y=23`