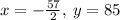Note: Your question sounds a little unclear, but I am assuming that your system of equations is:
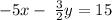
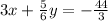
- It would anyways clear your concept because the procedure to find the solutions remains the same for any set of a system of equations.
Answer:
The solution of the system of equations be:
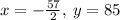
Explanation:
Given the system of equations
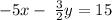
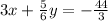
solving the system of equations
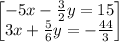
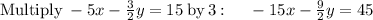
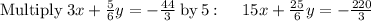
so the system of equations becomes
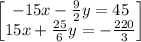
adding the equations
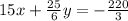

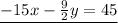
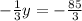
so
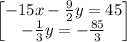
solving
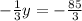 for y
for y
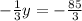
Multiply both sides by -3
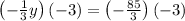
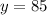
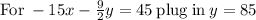
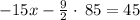
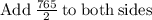
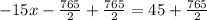
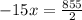
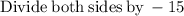
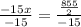
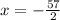
Therefore, the solution of the system of equations be: