Question

In triangle ACE, P is the centroid, PF = 6 , and AD = 15 15. Find the measures of PC and AP. Enter your answers as numbers.

Answer 1

PC = 12 units

AP = 10 units

Explanation:

• The centroid of a triangle is the intersection of the three medians of the triangle

• Each median connecting a vertex with the midpoint of the opposite side

• The centroid divides each median into two parts, which are always in the ratio 2: 1 from the vertex

In ΔACE

∵ P is the centroid of it

∴ P divides CF the ratio 2: 1 from C

∴ PC = 2 PF

∵ PF = 6 units

∴ PC = 2(6)

∴ PC = 12 units

∵ P divides AD at the ratio 2: 1 from A

→ That means AD = 2 + 1 = 3 parts, and AP =
`(2)/(3)` AD

∴ AP =
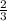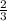`(2)/(3)` AD

∵ AD = 15 units

∴ AP = AP =
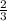`(2)/(3)` (15)

∴ AP = 10 units