Answer:
![P[at\ least\ 1] = 0.9961](https://img.qammunity.org/2021/formulas/mathematics/college/bv9g6qe23co80biu8fgvedz875vhsw17x4.png)
Explanation:
Given
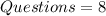
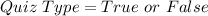
Required
Probability that s/he gets at least one correctly
First, we calculate the probability of answering a question correctly
Since, there are just 2 choices (true or false), the probability is:
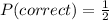
Similarly, the probability of answering a question, wrongly is:
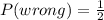
The following relationship exists, in probability:
![P[at\ least\ 1] = 1 - P[none]](https://img.qammunity.org/2021/formulas/mathematics/college/zglinj5tcaqmgmlkmu8gqkt8kjyux0tdv3.png)
So, to calculate the required probability.
First, we calculate the probability that he answers none of the 8 questions correctly.
![P[none] = p(wrong)^8](https://img.qammunity.org/2021/formulas/mathematics/college/7ozcxnbrri923k5e2buk8fkj817v8a4hte.png)
![P[none] = ((1)/(2))^8](https://img.qammunity.org/2021/formulas/mathematics/college/ua37gxbzxl01ftmqbesyt530smujg1opyx.png)
Substitute
![P[none] = ((1)/(2))^8](https://img.qammunity.org/2021/formulas/mathematics/college/ua37gxbzxl01ftmqbesyt530smujg1opyx.png) in
in
![P[at\ least\ 1] = 1 - P[none]](https://img.qammunity.org/2021/formulas/mathematics/college/zglinj5tcaqmgmlkmu8gqkt8kjyux0tdv3.png)
![P[at\ least\ 1] = 1 - ((1)/(2))^8](https://img.qammunity.org/2021/formulas/mathematics/college/u5jhxt22dfjbacl9wvd8vs8l8gsb4056nv.png)
![P[at\ least\ 1] = 1 - (1)/(256)](https://img.qammunity.org/2021/formulas/mathematics/college/uiz9zwjaer3xno0hvhack7fof6qs8rkrim.png)
Take LCM
![P[at\ least\ 1] = (256 - 1)/(256)](https://img.qammunity.org/2021/formulas/mathematics/college/z31uteh4h2iobbvcl3vwkekujkoieaob6o.png)
![P[at\ least\ 1] = (255)/(256)](https://img.qammunity.org/2021/formulas/mathematics/college/yeuklobvtmyb4ygryw6o9aixt3nf8w6q2t.png)
![P[at\ least\ 1] = 0.9961](https://img.qammunity.org/2021/formulas/mathematics/college/bv9g6qe23co80biu8fgvedz875vhsw17x4.png)
Hence, the probability that s/he gets at least one correctly is 0.9961