Question

On an eight question true-false quiz, a student guesses each answer. What is the probability that he/she gets at least one of the answers correct?

Answer 1

`P[at\ least\ 1] = 0.9961`

Explanation:

Given

`Questions = 8`

`Quiz\ Type = True\ or\ False`

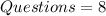
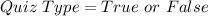
Required

Probability that s/he gets at least one correctly

First, we calculate the probability of answering a question correctly

Since, there are just 2 choices (true or false), the probability is:

`P(correct) = (1)/(2)`

Similarly, the probability of answering a question, wrongly is:

`P(wrong) = (1)/(2)`

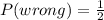
The following relationship exists, in probability:

`P[at\ least\ 1] = 1 - P[none]`

So, to calculate the required probability.

First, we calculate the probability that he answers none of the 8 questions correctly.

`P[none] = p(wrong)^8`

`P[none] = ((1)/(2))^8`

Substitute
`P[none] = ((1)/(2))^8` in
`P[at\ least\ 1] = 1 - P[none]`

`P[at\ least\ 1] = 1 - ((1)/(2))^8`

`P[at\ least\ 1] = 1 - (1)/(256)`

Take LCM

`P[at\ least\ 1] = (256 - 1)/(256)`

`P[at\ least\ 1] = (255)/(256)`

`P[at\ least\ 1] = 0.9961`

Hence, the probability that s/he gets at least one correctly is 0.9961