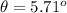Answer:
Step-by-step explanation:
In order to solve this problem, we mus start by drawing a free body diagram of the given situation (See attached picture).
From the free body diagram we can now do a sum of forces in the x and y direction. Let's start with the y-direction:
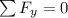
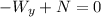
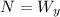
so:
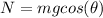
now we can go ahead and do a sum of forces in the x-direction:
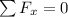
the sum of forces in x is 0 because it's moving at a constant speed.
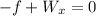
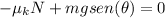
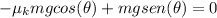
so now we solve for theta. We can start by factoring mg so we get:
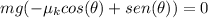
we can divide both sides into mg so we get:
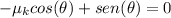
this tells us that the problem is independent of the mass of the object.
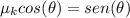
we now divide both sides of the equation into
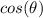 so we get:
so we get:
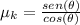
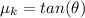
so we now take the inverse function of tan to get:

so now we can find our angle:

so