Answer:
(2,-17) should be the minimum.
Explanation:
The minimum of a quadratic function occurs at
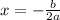 . If a is positive, the minimum value of the function is
. If a is positive, the minimum value of the function is

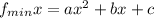 occurs at
occurs at
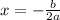
Find the value of
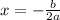
x = 2
evaluate f(2).
replace the variable x with 2 in the expression.

simplify the result.
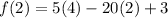
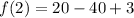

The final answer is -17
Use the x and y values to find where the minimum occurs.
HOPE THIS HELPS!