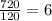Incomplete question. I Assumed the number of people is 6. In other words, In how many ways can 6 people be lined up to get on a bus if a particular person always boards the bus first or last?
Answer:
6
Explanation:
Note, this question involves the use of the permutation formula; which helps determine the arrangement or rearrangement of a set of objects in an ordered way. Since we are told a particular person (ie 1 person) from among the group always boards first or last, it forms our r.
P(n,r)=
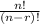 where n = number of people; r = the difference taken at a time.
where n = number of people; r = the difference taken at a time.
P(n,r) =
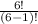 =
=