Question

According to the records of an electric company serving the Boston area, the mean electric consumption for all households during winter is 1650 kilowatt-hours per month. Assume that the monthly electric consumptions during winter by all households in this area have a normal distribution with a mean of 1650 kilowatt-hours and a standard deviation of kilowatt-hours. What percentage of 320 the households in this area have a monthly electric consumption of 1883 to 1975 kilowatt-hours

Answer 1

P(1833 < X < 1975) = 7.55%

Explanation:

From the given information:

Let X be the random variable that obeys a normal distribution and which represents the monthly electric consumption during winter by all households in the Boston area.

X
`\sim` N ( μ = 1650 , σ² = 320² )

The probability that a monthly consumption of 1883 to 1975 kilowatt is given as:

`P(1883 < X< 1975) = P( (1883 -1650)/(320) < Z< (1975-1650)/(320))`

`P(1883 <X< 1975) = P( (233)/(320) < Z< (325)/(320))`

`P(1883 < X<1975) = P( 0.728 < Z< 1.0156)`

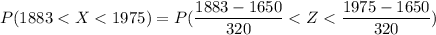
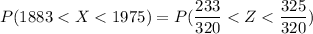
P(1833 < X < 1975) = P(Z< 1.0156) - P(Z< 0.738)

P(1833 < X < 1975) = 0.8452 - 0.7697

P(1833 < X < 1975) = 0.0755

P(1833 < X < 1975) = 7.55%