Answer:
The coordinates of the turning point will be:
The graph is also attached.
Explanation:
Given the expression
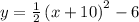
simplifying
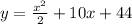
We know that the quadratic equation generally represents Parabola. We know that a turning point of the parabola of the quadratic equation depends upon the direction of the Parabola and the value of the leading coefficient.
The point, where the parabola tends to change the direction, is called the 'vertex'.
In other words, the vertex of the quadratic Parabola represents the turning point of the quadratic function.
Given the expression
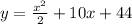
Parabola params are:
a = 1/2, b = 10, c = 44
As the leading coefficient = 1/2 which is less than 1, thus it represents the up-down facing Parabola.
Thus, the x-coordinate of the vertex:
x = -b/2a
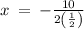
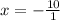
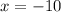
putting x = -10 in the original equation
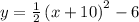
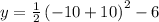
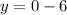
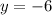
Therefore, the coordinates of the turning point will be:
The graph is also attached.