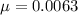Question

A 50.3-kg person, running horizontally with a velocity of 2.44 m/s, jumps onto a 13.4-kg sled that is initially at rest. (a) Ignoring the effects of friction during the collision, find the velocity of the sled and person as they move away. (b) The sled and person coast 30.0 m on level snow before coming to rest. What is the coefficient of kinetic friction between the sled and the snow

Answer 1

a

`v = 1.9267 \ m/s`

b

The value is
`\mu = 0.0063`

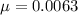
Step-by-step explanation:

From the question we are told that

The mass of the person is
`m_1 = 50.3 \ kg`

The horizontal velocity is
`u_1 = 2.44 \ m/s`

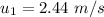
The mass of the shed is
`m_2 = 13.4 \ kg`

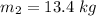
The distance covered is
`d = 30 \ m`

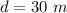
Generally from the law of momentum conservation we have that

`m_1 * u_1 + m_2 * u_2 = (m_1 + m_2)v`

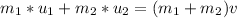
Here
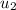`u_2` is the initial velocity of the shed which is 0 m/s

`50.3 * 2.44 + 13.4 * 0 = (50.3 + 13.4) v`

=>
`v = 1.9267 \ m/s`

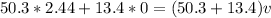
Generally the workdone by friction is mathematically represented as

`W = \Delta KE`

`W = (1)/(2) * m * (v_f - v )`

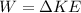
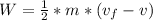
Here
`v_f` is the final velocity of the person and the shed when they come to rest and the value is
`v_f = 0 \ m/s`

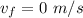
Generally this workdone by friction is also mathematically represented as

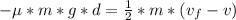
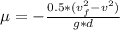
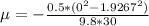
`W = - \mu * m * g * d`

=>
`- \mu * m * g * d = (1)/(2) * m * (v_f - v )`

=>
`\mu = - (0.5 * ( v_f^2 - v^2 ))/(g * d )`

=>
`\mu =- (0.5 * ( 0^2 - 1.9267^2 ))/(9.8 * 30 )`

=>
`\mu = 0.0063`