Question

Pls help me with these questions

Answer 1

Question # 7

x -1 0 1 2 3 4

y -5 1 7 13 19 25

From the table, it is clear that x and y change at a constant rate, it must be a linear function.

Determining the slope between the points (-1, -5) and (0, 1)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-1,\:-5\right),\:\left(x_2,\:y_2\right)=\left(0,\:1\right)`

`m=(1-\left(-5\right))/(0-\left(-1\right))`

`m=6`

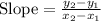
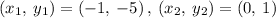
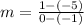
We know the y-intercept can be determined by setting x = 0 and solving for y.

From the graph, it is clear that

at x = 0, y = 1

Thus, the y-intercept = b = 1

We know the slope-intercept form of the line equation is

`y = mx+b`

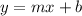
where m is the slope and b is the y-intercept

substituting m = 6 and b = 1 in the slope-intercept form

`y = mx+b`

`y = 6x + 1`

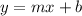
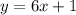
Therefore, the table represents the rule equation such as:

`y = 6x + 1`

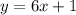
Question # 8

Given the table

Input Output

3 -5

2 -4

1 -3

2 -2

3 -1

We know that relation is said to be a function from a set X to a set of Y if each element of x is related to exactly one element in Y.

In other words, there must not be repeated 'x' element, meaning the value of 'x' must be unique.

It is clear from the table that the value of x is unique and there is no repetition of x, meaning each element of x is related to exactly one element in Y.

Thus, the given table represents the function.