Question

Can someone check whether its correct or no? this is supposed to be the steps in integration by parts​

Answer 1

`\displaystyle - \int (\sin(2x))/(e^(2x))\: \text{d}x=(\sin(2x))/(4e^(2x))+(\cos(2x))/(4e^(2x))+\text{C}`

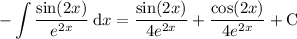
Explanation:

Fundamental Theorem of Calculus

`\displaystyle \int \text{f}(x)\:\text{d}x=\text{F}(x)+\text{C} \iff \text{f}(x)=\frac{\text{d}}{\text{d}x}(\text{F}(x))`

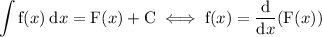
If differentiating takes you from one function to another, then integrating the second function will take you back to the first with a constant of integration.

Given integral:

`\displaystyle -\int (\sin(2x))/(e^(2x))\:\text{d}x`

`\textsf{Rewrite }(1)/(e^(2x)) \textsf{ as }e^(-2x) \textsf{ and bring the negative inside the integral}:`

`\implies \displaystyle \int -e^(-2x)\sin(2x)\:\text{d}x`

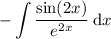
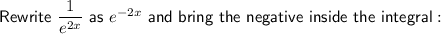
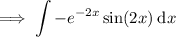
Use integration by parts.

`\boxed{\begin{minipage}{5 cm}\underline{Integration by parts} \\\\$\displaystyle \int u \frac{\text{d}v}{\text{d}x}\:\text{d}x=uv-\int v\: \frac{\text{d}u}{\text{d}x}\:\text{d}x$ \\ \end{minipage}}`

`\textsf{Let }\:u=\sin (2x) \implies \frac{\text{d}u}{\text{d}x}=2 \cos (2x)`

`\textsf{Let }\:\frac{\text{d}v}{\text{d}x}=-e^(-2x) \implies v=(1)/(2)e^(-2x)`

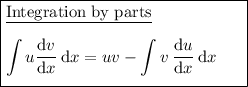
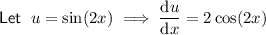
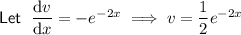
Substituting the defined parts into the formula:

`\begin{aligned}\implies \displaystyle -\int e^(-2x)\sin(2x)\:\text{d}x & =(1)/(2)e^(-2x)\sin (2x)- \int (1)/(2)e^(-2x) \cdot 2 \cos (2x)\:\text{d}x\\\\& =(1)/(2)e^(-2x)\sin (2x)- \int e^(-2x) \cos (2x)\:\text{d}x\end{aligned}`

`\displaystyle \textsf{For }\:-\int e^(-2x) \cos (2x)\:\text{d}x \quad \textsf{integrate by parts}:`

`\textsf{Let }\:u=\cos(2x) \implies \frac{\text{d}u}{\text{d}x}=-2 \sin(2x)`

`\textsf{Let }\:\frac{\text{d}v}{\text{d}x}=-e^(-2x) \implies v=(1)/(2)e^(-2x)`

`\begin{aligned}\implies \displaystyle -\int e^(-2x)\cos(2x)\:\text{d}x & =(1)/(2)e^(-2x)\cos(2x)- \int (1)/(2)e^(-2x) \cdot -2 \sin(2x)\:\text{d}x\\\\& =(1)/(2)e^(-2x)\cos(2x)+ \int e^(-2x) \sin(2x)\:\text{d}x\end{aligned}`

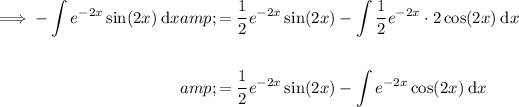
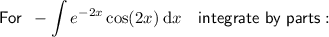
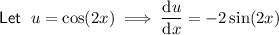
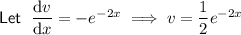
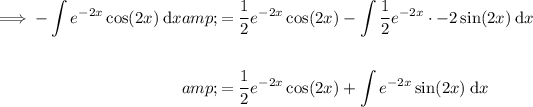
Therefore:

`\implies \displaystyle -\int e^(-2x)\sin(2x)\:\text{d}x =(1)/(2)e^(-2x)\sin (2x) +(1)/(2)e^(-2x)\cos(2x)+ \int e^(-2x) \sin(2x)\:\text{d}x`

`\textsf{Subtract }\: \displaystyle \int e^(-2x)\sin(2x)\:\text{d}x \quad \textsf{from both sides and add the constant C}:`

`\implies \displaystyle -2\int e^(-2x)\sin(2x)\:\text{d}x =(1)/(2)e^(-2x)\sin (2x) +(1)/(2)e^(-2x)\cos(2x)+\text{C}`

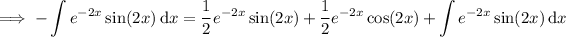
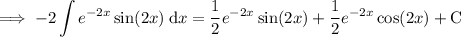
Divide both sides by 2:

`\implies \displaystyle -\int e^(-2x)\sin(2x)\:\text{d}x =(1)/(4)e^(-2x)\sin (2x) +(1)/(4)e^(-2x)\cos(2x)+\text{C}`

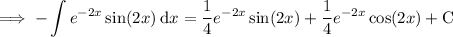
Rewrite in the same format as the given integral:

`\displaystyle \implies - \int (\sin(2x))/(e^(2x))\: \text{d}x=(\sin(2x))/(4e^(2x))+(\cos(2x))/(4e^(2x))+\text{C}`

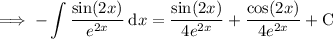
Differentiation Rules used:

`\boxed{\begin{minipage}{5.7 cm}\underline{Differentiating $\sin(k)$}\\\\If $y=\sin(kx)$, then $\frac{\text{d}y}{\text{d}x}=k\cos(kx)$\\\end{minipage}}`

`\boxed{\begin{minipage}{5.7 cm}\underline{Differentiating $\cos(k)$}\\\\If $y=\cos(kx)$, then $\frac{\text{d}y}{\text{d}x}=-k\sin(kx)$\\\end{minipage}}`

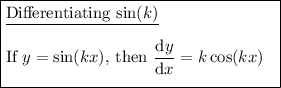
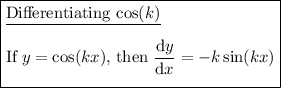
Integration Rules used:

`\boxed{\begin{minipage}{4 cm}\underline{Integrating $e^(kx)$}\\\\$\displaystyle \int e^(kx)\:\text{d}x=(1)/(k)e^(kx)+\text{C}$\end{minipage}}`