Question

Find the lenght of (a) using the pytoagorean theorem.
Longest line is 8
shortest line is 6

Answer 1

5.29

Explanation:

8

`\sqrt{8 { = }^(2) { - 6 {?}^(2) }^(2) }`

Answer 2

Answer: Missing side length (b) = 5.3 units

Explanation:

Hii, I'd love to help you out! (:

We are provided with two sides, which are:

• Longest side = 8
• Shortest side = 6

Luckily, there's a formula to find the third side!

The Pythagorean Theorem

The Pythagorean Theorem (
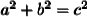`\pmb{a^2+b^2=c^2}`) is the formula that we will use to find the missing side. In this formula "a" and "b" denote the "legs" of the triangle (the two shorter sides) and "c" denotes the hypotenuse (the longest side which is opposite the right angle (the 90 degree angle)

NB: a and b are interchangeable, because a+b is the exact same thing as b+a; c is always the hypotenuse.

Now it's time for us to stick in the values.

`\bigstar\underbrace{\boxed{\sf a=6;\;c=8}}`

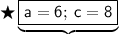
This is what we obtain upon sticking in the values:

`\tt 6^2+b^2=8^2`

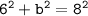
Now we can solve for b.

`\tt 36+b^2=64}\\b^2=64-36\\b^2=28\\b\approx5.3`

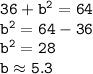
Thus, the value of "b" is 5.3. (Rounded to the nearest tenth, or one decimal place - one digit after the decimal point)

_____________

Hope I helped! Best wishes.

Reach far. Aim high. Dream big.

_____________

`\underbrace`