Question

Find the equation of the line specified. The line passes through the points (-2, 3) and (-4, 7) a. y = -2x - 1 b. y = -2x + 3 c. y = -4x - 1 d. y = -2x + 7 Please select the best answer from the choices provided A B C D. ​

Answer 1

Explanation:

To do this we will first use the slope formula to find the slope of the line. Given 2 points, you can't do anything else BUT find the slope. Always start there. The slope formula is:

`m=(y_2-y_1)/(x_2-x_1)`

Plugging in our values from the points where y2 is 7, y1 is 3, x2 is -4 and x1 is -2:

`m=(7-3)/(-4-(-2))=(7-3)/(-4+2)=(4)/(-2)=-2`

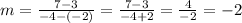
So the slope is -2. Now we will pick either point and use the x and y coordinates to fill in the point-slope form of a line, which is:

`y-y_1=m(x-x_1)`

where y1 and x1 are the coordinates from the point we pick, and m is the slope we just solved for. It doesn't matter which point you pick to use as your x and y coordinates; either one will give you the exact same equation...PROMISE!!

I chose (-2, 3), no reason in particular. x1 is -2 and y1 is 3:

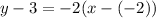`y-3=-2(x-(-2))` which simplifies a bit to

y - 3 = -2(x + 2) and a bit more to

y - 3 = -2x - 4 and even more to

y = -2x - 4 + 3 and finally to our final line in slope-intercept form:

y = -2x - 1

Choice a.