Question

A diffraction grating with 68 slits per cm is used to measure the wavelengths emitted by hydrogen gas.

A. At what angles in the fourth-order spectrum would you expect to find the two violet lines of wavelength 434 nm and of wavelength 410 nm?
B. What are the angles if the grating has 12,800 slits per cm?

Answer 1

a

`\theta _1 =0.687 ^o`

`\theta _2 =0.630 ^o`

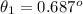
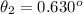
b

Generally given that the domain arcsine function is between -1 and 1 then the arcsine of 2.22 will not be valid

Generally given that the domain arcsine function is between -1 and 1 then the arcsine of 2.1 will not be valid

Step-by-step explanation:

From the question we are told that

The slit grating is
`N = 68 \ slits / cm = 6800 \ slits / m`

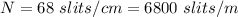
The order of spectrum is
`n = 4`

Generally the width of the slit is mathematically represented as

`a = (1)/( 6800)`

=>
`a = 0.000147 \ m`

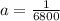
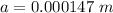
Generally the condition for constructive interference is

`asin\theta = n * \lambda`

Now for the first wavelength the angle is evaluated as

`\theta _1 = sin ^(-1) [ (n \lambda_1 )/(a) ]`

=>
`\theta _1 = sin ^(-1) [ (4* 434 *10^(-9) )/( 0.000147 ) ]`

=>
`\theta _1 =0.687 ^o`

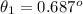
Now for the second wavelength the angle is evaluated as

`\theta _2 = sin ^(-1) [ (n \lambda_2 )/(a) ]`

=>
`\theta _2 = sin ^(-1) [ (4* 410 *10^(-9) )/( 0.000147 ) ]`

=>
`\theta _2 =0.630 ^o`

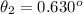
Gnerally if grating is
`N = 12800 \ slits per cm = 1280000 \ slits / m`

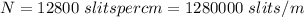
Generally the width of the slit is mathematically represented as

`a = (1)/( 1280000)`

=>
`a = 7.813 *10^(-7) \ m`

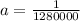
Generally the condition for constructive interference is

`asin\theta = n * \lambda`

Now for the first wavelength the angle is evaluated as

`\theta _1 = sin ^(-1) [ (n \lambda_1 )/(a) ]`

`\theta _1 = sin ^(-1) [ (4* 434 *10^(-9) )/( 7.813*10^(-7) ) ]`

=>
`\theta _1 = sin ^(-1) [ 2.22]`

Generally given that the domain arcsine function is between -1 and 1 then the arcsine of 2.22 will not be valid

=>
`\theta _1 =0.687 ^o`

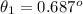
Now for the second wavelength the angle is evaluated as

`\theta _2 = sin ^(-1) [ (n \lambda_2 )/(a) ]`

=>
`\theta _2 = sin ^(-1) [ (4* 410 *10^(-9) )/( 7.813*10^(-7) ) ]`

=>
`\theta _2 = sin ^(-1) [2.1 ]`

Generally given that the domain arcsine function is between -1 and 1 then the arcsine of 2.22 will not be valid