Question

Consider △RST and △RYX.

Triangle R S T is shown. Line X Y is drawn parallel to side S T within triangle R S T to form triangle R Y X.

If the triangles are similar, which must be true?

StartFraction R Y Over Y S EndFraction = StartFraction R X Over X T EndFraction = StartFraction X Y Over T S EndFraction
StartFraction R Y Over R S EndFraction = StartFraction R X Over R T EndFraction = StartFraction X Y Over T S EndFraction
StartFraction R Y Over R S EndFraction = StartFraction R X Over R T EndFraction = StartFraction R S Over R Y EndFraction
StartFraction R Y Over R X EndFraction = StartFraction R S Over R T EndFraction = StartFraction X Y Over T S EndFraction

Answer 1

option B: StartFraction R Y Over R S EndFraction = StartFraction R X Over R T EndFraction = StartFraction X Y Over T S EndFraction

Answer 2

B. StartFraction R Y Over R S EndFraction = StartFraction R X Over R T EndFraction = StartFraction X Y Over T S EndFraction

i.e
`(RY)/(RS)` =
`(RX)/(RT)` =
`(XY)/(TS)`

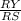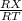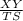
Explanation:

Two or more shape or figures are similar when their sides and angles can be compared appropriately.

In the given figure, ΔRXY is within ΔRST. Since the two triangles are similar, then their length of sides can be compared in the form of required ratios.

So that by comparison,

`(RY)/(RS)` =
`(RX)/(RT)` =
`(XY)/(TS)`

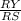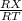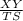
Therefore, the correct option to the question is B.