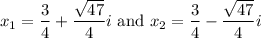Question

For the following equation: 2x^2 -3x + 7 = 0

(1) Calculate the discriminant
(2) Determine the number and type of solutions
(3) Use the quadratic formula to solve

Answer 1

the discriminant is b squared - 4 (a) (c) where a = 2, b = -3, and c = 7

after plugging in, the discrimimant is -47

if the discriminant is negative then it has no 'real' roots (the graph will not intersect the x-axis) but it has 2 solutions: (3+47i)/2 and (3-47i)/2 where 47i equals the square root of negative 47

Explanation:

Answer 2

Part 1)

`\Delta=-47`

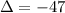
Part 2)

Since our discriminant is negative, we will have two complex (imaginary) solutions.

Part 3)

`\displaystyle x_1=(3)/(4)+(√(47))/(4)i\text{ and } x_2=(3)/(4)-(√(47))/(4)i`

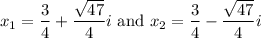
Explanation:

We have the equation:

`2x^2-3x+7=0`

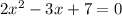
Labelling our coefficients, we see that:

`a=2, b=-3, \text{ and } c=7`

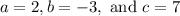
Part 1)

The discriminant (symbolized as Δ) is given by the formula:

`\displaystyle \Delta=b^2-4ac`

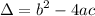
So, the value of our discriminant is:

`\displaystyle \Delta&=(-3)^2-4(2)(7)`

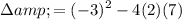
Evaluate:

`\Delta=9-56=-47`

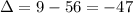
Part 2)

Remember the guidelines for the discriminant:

• If Δ>0 (the discriminant is positive), then our equation has two real solutions.
• If Δ<0 (the discriminant is negative), then our equation has two complex solutions (imaginary).
• If Δ=0 (the discriminant is 0), then our equation has exactly one real root.

Since our discriminant is a negative value, we will have two complex (imaginary) roots.

Part C)

The quadratic formula is given by:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

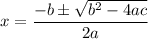
By substitution:

`\displaystyle x=(-(-3)\pm√((-3)^2-4(2)(7)))/(2(2))`

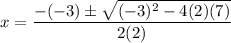
Evaluate:

`\displaystyle x=(3\pm√(-47))/(4)`

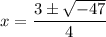
Simplify the square root:

`√(-47)=√(-1\cdot47)=i√(47)`

Therefore:

`\displaystyle x=(3\pm i√(47))/(4)`

Hence, our two zeros are:

`\displaystyle x_1=(3+i√(47))/(4)\text{ and } x_2=(3-i√(47))/(4)`

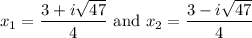
And in standard form:

`\displaystyle x_1=(3)/(4)+(√(47))/(4)i\text{ and } x_2=(3)/(4)-(√(47))/(4)i`