Question

A ​20-ft by ​the 40-ft rectangular swimming pool is surrounded by a walkway of uniform width. If the total area of the walkway is 256 ft2​, how wide is the​ walkway?

Answer 1

Answer: 2 feet

========================================================

Step-by-step explanation:

x = width of the walkway in feet

This is some positive real number.

The dimension of 20 feet bumps up to 20+2x when adding on x from both directions. Similarly, the 40 ft dimension becomes 40+2x

Refer to the diagram below.

The 20 ft by 40 ft pool is surrounded by a larger rectangle that is 20+2x ft by 40+2x ft

The pool itself is 20*40 = 800 sq ft. Add on the walkway area to get 800+256 = 1056 sq ft.

-----------

Area = length*width

1056 = (20+2x)*(40+2x)

1056 = 20*40 + 20*2x + 2x*40 + 2x*2x ... FOIL rule

1056 = 800 + 40x + 80x + 4x^2

0 = 4x^2 + 40x + 80x + 800 - 1056

0 = 4x^2 + 120x - 256

4x^2 + 120x - 256 = 0

4(x^2 + 30x - 64) = 0

x^2 + 30x - 64 = 0

Let's use the quadratic formula to finish solving for x.

Plug in a = 1, b = 30, c = -64

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-30\pm√((30)^2-4(1)(-64)))/(2(1))\\\\x = (-30\pm√(1156))/(2)\\\\x = (-30\pm34)/(2)\\\\x = (-30+34)/(2) \ \text{ or } \ x = (-30-34)/(2)\\\\x = (4)/(2) \ \text{ or } \ x = (-64)/(2)\\\\x = 2 \ \text{ or } \ x = -32\\\\`

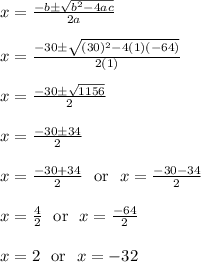
Recall we made x be positive. This is because a negative walkway width does not make sense. This means we'll ignore x = -32.

The only practical solution is x = 2

Therefore, the walkway is 2 feet wide