Question

A block of mass 4 kilograms is initially moving at 5m/s on a horizontal surface. There is friction between the block and the surface which causes the block to come to a complete stop. The coefficient of kinetic friction between the block and the surface is 0.5.

Calculate the distance the block slides while coming to a stop. Show all work.

Answer 1

d = 2.54 [m]

Step-by-step explanation:

Through the theorem of work and energy conservation, we can find the work that is done. Considering that the energy in the initial state is only kinetic energy, while the energy in the final state is also kinetic, however, this is zero since the body stops.

`E_(k1)+W=E_(k2)\\`

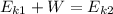
where:

W = work [J]

Ek1 = kinetic energy at initial state [J]

Ek2 = kinetic energy at the final state = 0.

We must remember that kinetic energy can be calculated by means of the following expression.

`(1)/(2) *m*v^(2)-W=0\\W= (1)/(2) *4*(5)^(2)\\W= 50 [J]`

We know that work is defined as the product of force by distance.

`W=F*d`

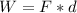
where:

F = force [N]

d = distance [m]

But the friction force is equal to the product of the normal force (body weight) by the coefficient of friction.

`f=m*g*0.5\\f = 4*9.81*0.5\\f = 19.62 [N]`

Now solving the equation for the work.

`d=W/F\\d = 50/19.62\\d = 2.54[m]`