Answer:
The angle between the two lines is 72.35° ⇒ to the nearest hundredth
Explanation:
- The angle between the two lines is the difference between their angles with the positive part of the x-axis (Ф = Ф
 - Ф
- Ф
 )
)
- The slope of the line equal to the tangent of the angle between the line and the positive part of the x-axis (m = tan Ф)
- The slope of the line whose equation is ax + by = c is m =

∵ The equation of the first line is 4x - 5y = 11
∴ a = 4 and b = -5
→ By using the 3rd rule of the slope above
∵ m
 =
=
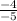 =
=
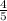
∴ m
 = 0.8
= 0.8
→ By using the 2nd rule above
∵ tan Ф
 = 0.8
= 0.8
∴ Ф
 =
=
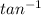 (0.8)
(0.8)
∴ Ф
 = 38.66° ⇒ to the nearest hundredth
= 38.66° ⇒ to the nearest hundredth
∵ The equation of the first line is 2x + 3y = 7
∴ a = 2 and b = 3
→ By using the 3rd rule of the slope above
∵ m
 =
=

∴ m
 =
=

→ By using the 2nd rule above
∵ tan Ф
 =
=

∴ Ф
 =
=
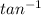 (
(
 )
)
∴ Ф
 = -33.69° ⇒ to the nearest hundredth
= -33.69° ⇒ to the nearest hundredth
→ By using the 1st rule above
∵ Ф = -33.69 - 38.66
∴ Ф = -72.35°
→ Ignore the negative sign
∴ The angle between the two lines is 72.35° ⇒ to the nearest hundredth
V.I.N:
You can use this rule to find the angle between 2 lines tan Ф = I
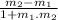 I
I