The product of
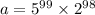 and
and
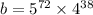 is
is
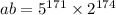 , resulting in 120 digits when expressed as an ordinary number.
, resulting in 120 digits when expressed as an ordinary number.
1. Express a and b in their prime factorization form:
![\[ a = 5^(99) * 2^(98) \] \[ b = 5^(72) * 4^(38) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/68qypwl57y0eez2ekffi7higi72r2x02mu.png)
Note that
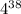 can be expressed as
can be expressed as
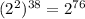 .
.
2. Multiply a and b to find ab:
![\[ ab = (5^(99) * 2^(98)) * (5^(72) * 2^(76)) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/afbjzwt0z438qmv8kbl7jwjz72aj2a2xan.png)
Combine the like terms:
![\[ ab = 5^(99 + 72) * 2^(98 + 76) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xjdank5314k9tsws8y40qcr9j71441stdi.png)
Simplify the exponents:
![\[ ab = 5^(171) * 2^(174) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/w9cdjg8zv216kp0fxrmxpez6lwno638k5e.png)
3. To find the number of digits in ab, we can use the formula:
![\[ \text{Number of digits} = \lfloor \log_(10)(ab) \rfloor + 1 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1ree83m2sdy5qsts4pwebhtbkp7r0gnhy5.png)
Using this formula:
![\[ \text{Number of digits} = \lfloor \log_(10)(5^(171) * 2^(174)) \rfloor + 1 \] \[ \text{Number of digits} = \lfloor 171 \cdot \log_(10)(5) + 174 \cdot \log_(10)(2) \rfloor + 1 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/sugqgx4euauutt757p6chgas4kslb4dbse.png)
4. Calculate the value:
![\[ \text{Number of digits} \approx \lfloor 171 \cdot 0.69897 + 174 \cdot 0.30103 \rfloor + 1 \] \[ \text{Number of digits} \approx \lfloor 119.52467 \rfloor + 1 \] \[ \text{Number of digits} = 119 + 1 \] \[ \text{Number of digits} = 120 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5fqsf7esa550yyanv32zvgnga291okdjbt.png)
Therefore, ab has 120 digits when written as an ordinary number.