Question

Solve by using elimination. Express your answer as an ordered pair.

Answer 1

Greetings again.

The answer is (-2,0)

Step-by-step explanation:

This one is different from other 2 previous questions. The last and previous 2 questions have positive y for another equation and negative y for another equation which makes them 0 (As y - y = 0)

But this one is different. y-terms both are negative for both equations. If we decide to add -2y and -2y then It'd make -4y which doesn't make 0.

And how are we gonna solve by elimination? That's simple. By multiplying one of the equation by -1.

We can do that, to eliminate y-term out. Choose one equation to multiply. I'll be multiplying -1 in the first equation.

`-x-2y=2`

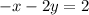
Multiply -1 in whole equation.

`-x(-1)-2y(-1)=2(-1)\\x+2y=-2`

Remind that negative multiply/distribute in negative equal positive always.

And x + 2y = -2 is your new equation from the first equation.

`\left \{ {{x+2y=-2} \atop {4x-2y=-8}} \right.`

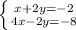
This is our new equations. Then we are able to eliminate y-term.

`5x=-10\\x=-2`

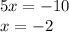
In case if you forget again, we can simply add/subtract vertically.

x+4x = 5x

2y-2y = 0

-2-8 = -10

That's how we get 5x=-10 and thus x = -2.

We already get x-value, and you know that we need to find the y-value too.

Therefore, substitute x = -2 in any given equations. Less coefficient value, the faster and better.

I'll substitute in -x-2y=2

`-x-2y=2`

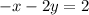
Substitute x = -2 in the equation.

`-(-2)-2y=2\\2-2y=2\\-2y=2-2\\-2y=0\\y=(0)/(-2)\\y=0`

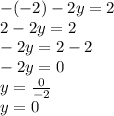
Thus, when x = -2, y = 0. Since you want the answer as ordered pair, then the answer is (-2,0)

Answer 2

(-2, 0)

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

Algebra I

• Solving systems of equations using substitution/elimination

Step-by-step explanation:

Step 1: Define Systems

-x - 2y = 2

4x - 2y = -8

Step 2: Rewrite Systems

-x - 2y = 2

1. Multiply both sides by -1: x + 2y = -2

Step 3: Redefine Systems

x + 2y = -2

4x - 2y = -8

Step 4: Solve for x

Elimination

1. Combine equations: 5x = -10
2. Divide 5 on both sides: x = -2

Step 5: Solve for y

1. Define equation: 4x - 2y = -8
2. Substitute in x: 4(-2) - 2y = -8
3. Multiply: -8 - 2y = -8
4. Isolate y term: -2y = 0
5. Isolate y: y = 0