Question

What is the largest possible integral value in the domain of the real-valued function

f(x)=
`(1)/(√(800-2x) )`

Answer 1

Max Value: x = 400

General Formulas and Concepts:

Algebra I

• Domain is the set of x-values that can be inputted into function f(x)

Calculus

• Antiderivatives
• Integral Property:
  `\int {cf(x)} \, dx = c\int {f(x)} \, dx`
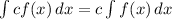
• Integration Method: U-Substitution
• [Integration] Reverse Power Rule:
  `\int {x^n} \, dx = (x^(n+1))/(n+1) + C`

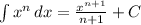
Explanation:

Step 1: Define

`f(x) = (1)/(√(800-2x) )`

Step 2: Identify Variables

Using U-Substitution, we set variables in order to integrate.

`u = 800-2x\\du = -2dx`

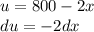
Step 3: Integrate

1. Define:
   `\int {f(x)} \, dx`
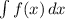
2. Substitute:
   `\int {(1)/(√(800-2x) ) } \, dx`
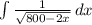
3. [Integral] Int Property:
   `-(1)/(2) \int {(-2)/(√(800-2x) ) } \, dx`
4. [Integral] U-Sub:
   `-(1)/(2) \int {(1)/(√(u) ) } \, du`
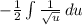
5. [Integral] Rewrite:
   `-(1)/(2) \int {u^{-(1)/(2) }} \, du`
6. [Integral - Evaluate] Reverse Power Rule:
   `-(1)/(2)(2√(u)) + C`
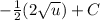
7. Simplify:
   `-√(u) + C`
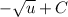
8. Back-Substitute:
   `-√(800-2x) + C`
9. Factor:
   `-√(-2(x - 400)) + C`

Step 4: Identify Domain

We know from a real number line that we cannot have imaginary numbers. Therefore, we cannot have any negatives under the square root.

Our domain for our integrated function would then have to be (-∞, 400]. Anything past 400 would give us an imaginary number.