Answer:
The added term needed for that expression to be a square is 9/16.
Explanation:
We're provided with two terms, and asked to add an additional term to make this a perfect square. For this to work, the term needs to be a scalar value that is the square of half the coefficient of the second term.
That coefficient is 3/2, so half of that is 3/4, and its square is 9/16.
If we tack that on the end then, we get:
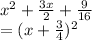
To confirm the answer, let's expand it and see if we get the original expression:
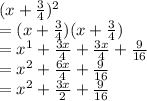
So 9/16ths is the scalar that needs to be added on the end.