Question

I need help asap !!​

Answer 1

Solving the expression
`\frac{\sqrt[3]{7} }{\sqrt[5]{7} }` we get
`\mathbf{7^{(2)/(15)}}`

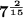
Option D is correct option.

Explanation:

We need to solve the expression:
`\frac{\sqrt[3]{7} }{\sqrt[5]{7} }`

We know that

`\sqrt[3]{x}=x^{(1)/(3)` and
`\sqrt[5]{x}=x^{(1)/(5)`

Using above rule:

`\frac{\sqrt[3]{7} }{\sqrt[5]{7} }\\=\frac{7^{(1)/(3)}}{7^{(1)/(5)}}`

Now, we know the exponent rule if bases are same and divided then exponents are subtracted i.e:
`(a^m)/(a^n)=a^(m-n)`

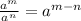
Using the exponent rule

`=7^{(1)/(3)-(1)/(5) }\\Simplifying\:exponents\\=7^{(5-3)/(15)}\\=7^{(1*5-1*3)/(15)}\\=7^{(2)/(15)}`

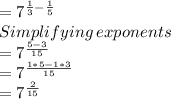
So, solving the expression
`\frac{\sqrt[3]{7} }{\sqrt[5]{7} }` we get
`\mathbf{7^{(2)/(15)}}`

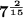
Option D is correct option.