Question

A stationary 500 kg tank fires a 20 kg miegile at 100 m/s. What is the velocity of the tank after the missile is fired? Assume the brakes are not on and there is no friction.​

Answer 1

v₁ = 4 [m/s].

Step-by-step explanation:

This problem can be solved by using the principle of conservation of linear momentum. Where momentum is preserved before and after the missile is fired.

`P=m*v`

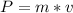
where:

P = linear momentum [kg*m/s]

m = mass [kg]

v = velocity [m/s]

`(m_(1)*v_(1))=(m_(2)*v_(2))`

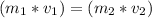
where:

m₁ = mass of the tank = 500 [kg]

v₁ = velocity of the tank after firing the missile [m/s]

m₂ = mass of the missile = 20 [kg]

v₂ = velocity of the missile after firing = 100 [m/s]

`(500*v_(1))=(20*100)\\v_(1)=2000/500\\v_(1)=4[m/s]`