Question

Tell weather the lines for each pair of equations are parallel perpendicular or neither y=-1/5x+6

-2x+10y=5

Answer 1

The slopes are neither perpendicular nor parallel.

Explanation:

First we are going to find the slope-inercept form from the equation, -2x + 10y = 5.

Solve for y.

-2x + 10y = 5

+2x. = +2x

10y = 2x + 5

`\begin{gathered} (10y)/(10) = (2x + 5)/(10) \\ y = (1)/(5)x + (1)/(2) \end{gathered}`

So we now have

`\begin{gathered}y = (1)/(5)x + (1)/(2) \\ and \\ y = - (1)/(5) x + 6 \end{gathered}`

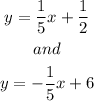
Looking at the equation above, the slopes are neither perpendicular nor parallel.