Question:
A fastball is hit straight up over home plate. The ball's height, h (in feet), from the ground is modeled by h(t)=-16t^2+80t+5, where t is measured in seconds. Write an equation to determine how long it will take for the ball to reach the ground.
Answer:
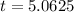
Explanation:
Given
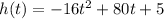
Required
Find t when the ball hits the ground
This implies that h(t) = 0
So, we have:

Reorder
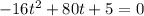
Using quadratic formula, we have:

Where
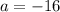
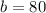
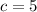
So, we have:
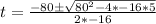
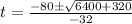
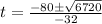
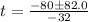
This gives:
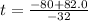 or
or
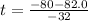
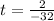 or
or

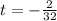 or
or
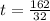
But time can not be negative.
So, we have:
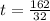
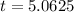
Hence, time to hit the ground is 5.0625 seconds