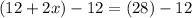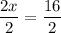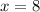Answer:
x=8
Explanation:
Visualize the points X Y and Z. X and Z form a line, and Y is between them (on the same line).
Several distances are given, some as numbers, one as an expressions containing "x".
By the segment addition postulate, the two small line segments add up to the larger line segment:
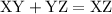
Substituting:
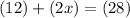
Then, use algebra to solve for x. Note that "x" only appears once, so to solve for "x", we only need to isolate it (undo the things connected to it).
There are two things done to "x". Multiplying by 2, and Adding 12. Since multiplication normally happens before addition, to undo these things, we must undo the addition first, then undo the multiplication: