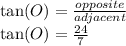Answer:
a. sin(M)=7/25
b. cos(M)=24/25
c. tan(M)=7/24
d. sin(O)=24/25
e. cos(O)=7/25
f. tan(O)=24/7
Explanation:
Pythagorean Theorem
Note that for the given triangle, one side length is not given, so that will need to be solved for. Since the triangle is a right triangle, the Pythagorean theorem applies:
 where c is the hypotenuse, and "a" and "b" are the two legs.
where c is the hypotenuse, and "a" and "b" are the two legs.

Since "b" is a length of a leg of the triangle, we assume it positive and reject the negative solution.
Thus, the missing side is 24 units long.
Trigonometric Definitions
For this problem, remember that trigonometric functions take in an angle, and output a ratio of sides.
So, it is then important to remember which two sides each trigonometric function uses to make its ratio of sides. Many people remember this with SohCahToa, where the bolded letters represent one of the three trig functions, and the other two letter represent one of the sides of the right triangle
- h: hypotenuse (the side across from the right angle)
- o: opposite (the side across from the angle input to the trig function)
- a: adjacent (the side that isn't the hypotenuse, touching the angle
So:

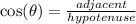
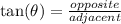
So, for each situation, identify which angle is going into the function, then identify which sides you need and where they are. Substitute and simplify.
Evaluating Trigonometric functions
a. sin(M)
Note that here the input angle is angle M. The hypotenuse is always across from the right angle, so the hypotenuse is side MO=25. The adjacent here is MN=24 (the side touching angle M that isn't the hypotenuse), and the opposite side is ON=7 (the side not touching the angle M)
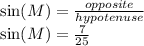
b. cos(M)
Again, the input angle is angle M, so the side definitions are the same as in part a.
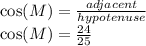
c. tan(M)
Again, the input angle is angle M, so the side definitions are the same as in part a & b.
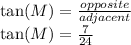
d. sin(O)
Here, the input angle is angle is different from the previous parts of the problem, so we need to look back at our triangle and determine which side is which.
The input angle is angle O. The hypotenuse is always across from the right angle, so the hypotenuse is side MO=25. The adjacent here is ON=7 (the side touching angle O that isn't the hypotenuse), and the opposite side is MN=24 (the side not touching the angle O)

e. cos(M)
Again, the input angle is angle O, so the side definitions are the same as in part d.
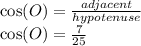
f. tan(M)
Again, the input angle is angle O, so the side definitions are the same as in part d & e.