Answer:

Step-by-step explanation:
The average rate of change can be found by using the following formula

Since the interval goes from -7 to 2, we should find the y-values that correspond to x=-7 and x=2.
By inspection of the graph, we can clearly see that when x is -7, y is -7 as well and when x is 2, y is 5.
Now that we know this, we can simply plug these values into the formula!
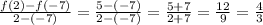
Good luck!