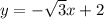Answer:
Explanation:
We want to find the equation of a straight line that cuts off an intercept of two from the y-axis and whose perpendicular distance from the origin is one.
Let Point M be (x, y). As we know, Point R will be (0, 2) and Point O (the origin) will be (0, 0).
First, we can use the distance formula to determine values for M. The distance formula is given by:
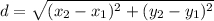
Since we know that the distance between O and M is one, d = 1:
And we will let M(x, y) be (x₂, y₂) and O(0, 0) be (x₁, y₁). So:
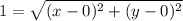
Simplify:
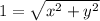
We can solve for y. Square both sides:

Rearranging gives:
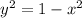
Take the square root of both sides. Since M is in the first quadrant, we only need to worry about the positive case. Therefore:
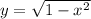
So, Point M is now given by (we substitute the above equation for y):
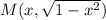
We know that Segment OM is perpendicular to Line RM.
Therefore, their slopes will be negative reciprocals of each other.
So, let’s find the slope of each segment/line. We will use the slope formula given by:
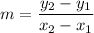
Segment OM:
For OM, we have two points: O(0, 0) and M(x, √(1-x²)). So, the slope will be:

Line RM:
For RM, we have the two points R(0, 2) and M(x, √(1-x²)). So, the slope will be:
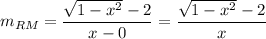
Since their slopes are negative reciprocals of each other, this means that:
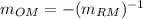
Substitute:
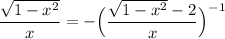
Now, we can solve for x. Simplify:

Cross-multiply:
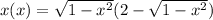
Distribute:
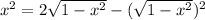
Simplify:
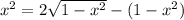
Distribute:
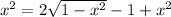
So:
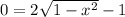
Adding 1 and then dividing by 2 yields:
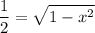
Then:
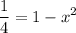
Therefore, the value of x is:
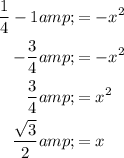
Then, Point M will be:
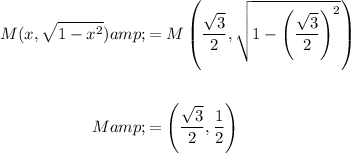
Therefore, the slope of Line RM will be:
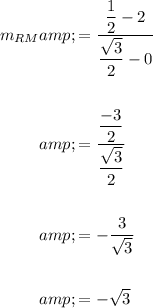
And since we know that R is (0, 2), R is the y-intercept of RM. Then, using the slope-intercept form:

We can see that the equation of Line RM is: