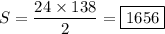There's a fixed difference of 6 between terms (9 - 3 = 6, 15 - 9 = 6, and so on). The first term of the sequence is 3, so the
 -th term is
-th term is
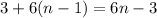
If there are 24 terms in the sum, then the last term is 6×23 - 3 = 135.
Let
 be the sum,
be the sum,

Reverse the order of terms:
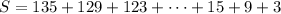
If we add up the terms in the same positions, we get twice
 on the left side, while on the right side we observe that each pair of terms will sum to 138.
on the left side, while on the right side we observe that each pair of terms will sum to 138.

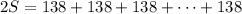
and since there are 24 terms in the sum, the right side is the sum of 24 copies of 138. In other words,

and solving for
 gives
gives