The zeros of the polynomial function
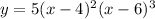 and their multiplicities are:
and their multiplicities are:
4 with multiplicity 2
6 with multiplicity 3
The multiplicity of a zero is the number of times it appears in the factored form of the polynomial. In this case, the factor (x−4) appears twice, so the zero at x=4 has multiplicity 2. The factor (x−6) appears three times, so the zero at x=6 has multiplicity 3.
To find the zeros of a polynomial, we can set the polynomial equal to zero and solve the resulting equation. In this case, we have:

This equation is true if any of the factors is equal to zero. So, we have three equations to solve:
x-4 = 0
x-6 = 0
x-6 = 0
The first equation has the solution x=4. The second equation has the solution x=6. The third equation has the solution x=6.
Therefore, the zeros of the polynomial are x=4 and x=6. The zero at x=4 has multiplicity 2 and the zero at x=6 has multiplicity 3.