Question

Thermodynamics fill in the blanks The swimming pool at the local YMCA holds roughly 749511.5 L (749511.5 kg) of water and is kept at a temperature of 80.6 °F year round using a natural gas heater. If you were to completely drain the pool and refill the pool with 50°F water, (blank) GJ (giga-Joules) of energy are required to to heat the water back to 80.6 °F. Note: The specific heat capacity of water is 4182 J/kg ⋅°C. The cost of natural gas per GJ is $2.844. It costs $ (blank) to heat the pool (to the nearest dollar).

Answer 1

`95.914\ \text{GJ}`

`\$272.78`

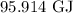
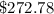
Step-by-step explanation:

m = Mass of water = 749511.5 kg

c = Specific heat of water = 4182 J/kg ⋅°C

`\Delta T` = Change in temperature =
`80.6-50=30.6^(\circ)\text{F}`

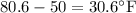
Cost of 1 GJ of energy = $2.844

Heat required is given by

`Q=mc\Delta T\\\Rightarrow Q=749511.5* 4182* 30.6\\\Rightarrow Q=95.914* 10^9\ \text{J}=95.914\ \text{GJ}`

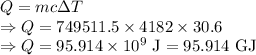
Amount of heat required to heat the water is
`95.914\ \text{GJ}`.

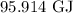Cost of heating the water is

`95.914* 2.844=\$272.78`

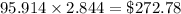
Cost of heating the water to the required temperature is
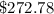`\$272.78`.