Question

I have these factoring questions I need help with.

Answer 1

`f(x)=4x^2+4x-3`

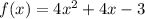
1. Determine y-intercept.

The y-intercept is (0,-3). Substitute x = 0 in the equation as we get f(x) = -3 as the y-intercept.

2. Determine the zeros.

Factor the polynomials first.
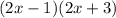`(2x-1)(2x+3)` This is the factored form. The zeros are the roots of equation. Therefore, the zeros are 1/2 and -3/2

3. Determine the Axis of Symmetry

We can solve this by using the formula of
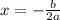`x=-(b)/(2a)` However, I'll be solving the Axis of Symmetry with Calculus instead.

`f'(x)=2(4x^(2-1))+1(4x^(1-1))-0\\f'(x)=8x+4`

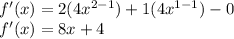
Then let f'(x) = 0 to find the Axis of Symmetry.

`8x+4=0\\8x=-4\\x=-(4)/(8)\\x=-(1)/(2)`

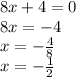
Therefore, the Axis of Symmetry is -1/2

4. Determine the vertex.

Substitute the value of Axis of Symmetry in f(x).

`f(x)=4(-(1)/(2))^2+4(-(1)/(2))-3\\f(x)=4((1)/(4))-2-3\\f(x)=1-2-3\\f(x)=-4`

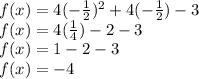
Therefore the vertex is at (-1/2, -4)

5. Does the vertex representing max-pont or min-point?

The vertex represents the minimum point. The graph is upward, meaning the minimum point is the point that gives the LOWEST Y-VALUE.

7. Graph f(x)

Unfortunately I won't be able to graph. But I can tell you to graph a parabola that has the most curve at the vertex and intercepts y-axis at (0,-3).

--------------------------- End of Part 1 --------------------------------

2. Write the general form of Quadratic Function in standard form.

`y=ax^2+bx+c`

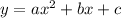
The graph can be easily determined about the y-intercept and being an upward or downward parabola along with how narrow or wide the parabola is.

For example, c value is the y-intercept as defined. When a > 0, the parabola is upward and when a < 0, the parabola is downward. The more value of | a | is, the more narrow it will be and the less value of | a | it is, the wider it will be.

3. Write in Factored Form

`y=(x+a)(x+b)\\y=(x-a)(x-b)\\y=(x+a)(x-b)\\y=(x-a)(x+b)`

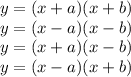
These are factored forms with different types of operators.

The equation can be easily determined about the roots of equation. For example, if the function is in f(x) = (x+2)(x-1) Then the roots would be x = -2 and 1 as the graph will intercept x-axis at (-2,0) and (1,0)

4. Write in Vertex Form.

`y=a(x-h)^2+k`

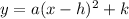
The equation can be easily determined for the vertex, axis of symmetry and the same narrow/wide/upward/downward parabola again.

The vertex is at (h,k) and the axis of symmetry is at x = h.

For example,
`y=(x-2)^2+3`

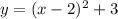
The vertex would be at (2,3) and the axis of symmetry is x = 2.