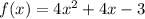
1. Determine y-intercept.
The y-intercept is (0,-3). Substitute x = 0 in the equation as we get f(x) = -3 as the y-intercept.
2. Determine the zeros.
Factor the polynomials first.
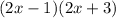 This is the factored form. The zeros are the roots of equation. Therefore, the zeros are 1/2 and -3/2
This is the factored form. The zeros are the roots of equation. Therefore, the zeros are 1/2 and -3/2
3. Determine the Axis of Symmetry
We can solve this by using the formula of
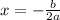 However, I'll be solving the Axis of Symmetry with Calculus instead.
However, I'll be solving the Axis of Symmetry with Calculus instead.

Then let f'(x) = 0 to find the Axis of Symmetry.
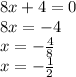
Therefore, the Axis of Symmetry is -1/2
4. Determine the vertex.
Substitute the value of Axis of Symmetry in f(x).

Therefore the vertex is at (-1/2, -4)
5. Does the vertex representing max-pont or min-point?
The vertex represents the minimum point. The graph is upward, meaning the minimum point is the point that gives the LOWEST Y-VALUE.
7. Graph f(x)
Unfortunately I won't be able to graph. But I can tell you to graph a parabola that has the most curve at the vertex and intercepts y-axis at (0,-3).
--------------------------- End of Part 1 --------------------------------
2. Write the general form of Quadratic Function in standard form.

The graph can be easily determined about the y-intercept and being an upward or downward parabola along with how narrow or wide the parabola is.
For example, c value is the y-intercept as defined. When a > 0, the parabola is upward and when a < 0, the parabola is downward. The more value of | a | is, the more narrow it will be and the less value of | a | it is, the wider it will be.
3. Write in Factored Form
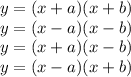
These are factored forms with different types of operators.
The equation can be easily determined about the roots of equation. For example, if the function is in f(x) = (x+2)(x-1) Then the roots would be x = -2 and 1 as the graph will intercept x-axis at (-2,0) and (1,0)
4. Write in Vertex Form.

The equation can be easily determined for the vertex, axis of symmetry and the same narrow/wide/upward/downward parabola again.
The vertex is at (h,k) and the axis of symmetry is at x = h.
For example,
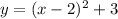
The vertex would be at (2,3) and the axis of symmetry is x = 2.