Answer:
The age of the sample is
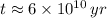 . It is possible, since the definition of half-life is the time taken by the isotope to halve its mass.
. It is possible, since the definition of half-life is the time taken by the isotope to halve its mass.
Step-by-step explanation:
All radioactive isotopes decays exponentially, the decay is represented by the following formula:
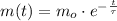 (1)
(1)
Where:
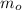 - Initial mass of the isotope, measured in grams.
- Initial mass of the isotope, measured in grams.
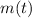 - Current mass of the isotope, measured in grams.
- Current mass of the isotope, measured in grams.
 - Time, measured in years.
- Time, measured in years.
 - Time constant, measured in years.
- Time constant, measured in years.
Now we clear the time of the isotope within the formula:
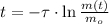
In addtion, the time constant can be calculated in terms of the half-life (
 ), measured in years:
), measured in years:
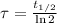 (2)
(2)
If we know that
 ,
,
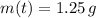 and
and
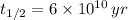 , then the age of the isotope is:
, then the age of the isotope is:
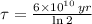
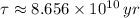

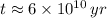
The age of the sample is
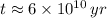 . It is possible, since the definition of half-life is the time taken by the isotope to halve its mass.
. It is possible, since the definition of half-life is the time taken by the isotope to halve its mass.