Answer:
r = 3.797 cm
h = 7.594 cm
Explanation:
The cylinder volume V = πr² h
So, given that the volume = 344 ml
Then,
344 = πr² h
Make h the subject of the formula:
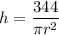 ----- (1)
----- (1)
Similarly, the surface area of a cylinder is expressed by:
A = 2πr² h + 2 πr² ---- (2)
If we replace the value of h from above in (1) to (2)
Then;

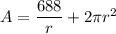
Taking the differential of A with respect to r, we have:
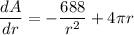
Set
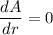 for the minimum surface area.
for the minimum surface area.
So,
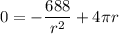
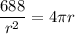
Divide both sides by 4
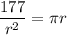
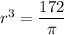
![r = \sqrt[3]{(172)/(\pi)}](https://img.qammunity.org/2021/formulas/mathematics/college/xtpgc67imyltki4541tall6a52s8g9ofmr.png)
r = 3.797 cm
From (1), the height is:
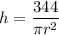
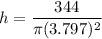
h = 7.594 cm