Hello! :)
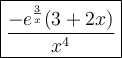
Find the derivative using the quotient rule:
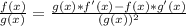
In this instance:
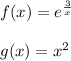
Use the following properties to find the derivative of f(x) and g(x):
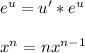
Use the quotient rule:
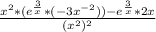
Simplify the numerator:
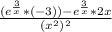
Factor out
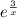
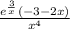
Factor out -1 from the numerator:
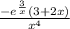
And we're done! Thanks for posting the question to my 1000th answer!