Question

Algebraically, find all remaining zeros of f(x) = 8x^3 - 6x^2-36x +27 in simplest form.

Answer 1

`x={-(3√(2))/(2), (3)/(4), (3√(2))/(2)}`

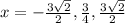
Explanation:

In order to find the zeros of a function, we must first set the equation equal to zero, so we get:

`8x^(3)-6x^(2)-36x+27=0`

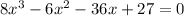
so we can now solve this by factoring. We can factor this equation by grouping. We start by grouping the equation in pairs of terms, so we get:

`(8x^(3)-6x^(2))+(-36x+27)=0`

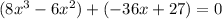
and factor each group, so we get:

`2x^(2)(4x-3)-9(4x-3)=0`

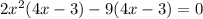
and now factor again, so we get:

`(2x^(2)-9)(4x-3)=0`

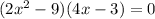
and now we set each of the factors equal to zero to find the zeros:

`2x^(2)-9=0`

`2x^(2)=9`

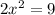
we divide both sides into 2 to get:

`x^(2)=(9)/(2)`

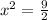
and take the square root to both sides to get:

`x=\pm\sqrt{(9)/(2)}`

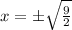
which yields:

`x=\pm(3)/(√(2))`

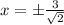
We rationalize so we get:

`x=\pm(3√(2))/(2)`

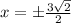
this means that we have two zeros here:

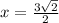`x=(3√(2))/(2)` and
`x=-(3√(2))/(2)`

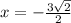
so we take the other factor and set it equal to zero.

4x-3=0

and solve for x

4x=3

`x=(3)/(4)`

and that will be our third zero.