Answer:
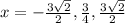
Explanation:
In order to find the zeros of a function, we must first set the equation equal to zero, so we get:
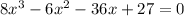
so we can now solve this by factoring. We can factor this equation by grouping. We start by grouping the equation in pairs of terms, so we get:
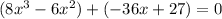
and factor each group, so we get:
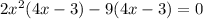
and now factor again, so we get:
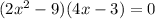
and now we set each of the factors equal to zero to find the zeros:
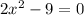
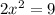
we divide both sides into 2 to get:
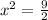
and take the square root to both sides to get:
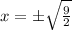
which yields:
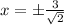
We rationalize so we get:
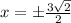
this means that we have two zeros here:
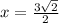 and
and
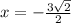
so we take the other factor and set it equal to zero.
4x-3=0
and solve for x
4x=3
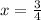
and that will be our third zero.