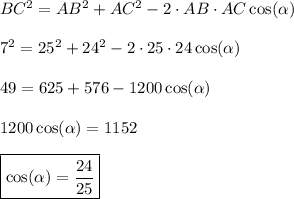Answer:
cos(α) = 24/25.
Explanation:
First of all, we'll find the answer just using the fact that ABC is a right triangle in C. So, by the definition of cosine:
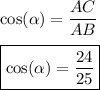
Now, we'll solve the question with another approach. By the Law of Cosines in the triangle ABC: