Answer:

Explanation:
We have the equation:
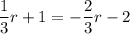
And we would like to solve for r.
First, we can multiply both sides by the denominator 3. This will remove the fractions. So:

Distribute:
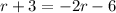
Now, we can add 2r to both sides:
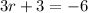
And we can also subtract 3 from both sides:
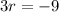
Finally, we can divide both sides by 3 to get:
