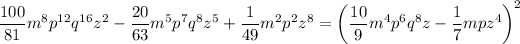Answer:
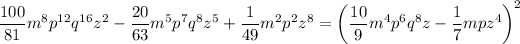
Explanation:
Trinomio Cuadrado Perfecto
El producto notable llamado cuadrado de un binomio se expresa como:
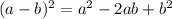
Si se tiene un trinomio, es posible convertirlo en un cuadrado perfecto si cumple con las condiciones impuestas en la fórmula:
* El primer término es un cuadrado perfecto
* El último término es un cuadrado perfecto
* El segundo término es el doble del proudcto de los dos términos del binomio.
Tenemos la expresión:
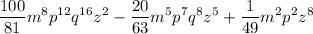
Calculamos el valor de a como la raiz cuadrada del primer término del trinomio:
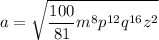
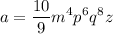
Calculamos el valor de a como la raiz cuadrada del primer término del trinomio:
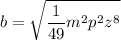
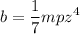
Nos cercioramos de que el término central es 2ab:
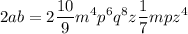
Operando:
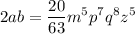
Una vez verificado, ahora podemos decir que: