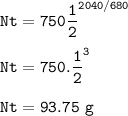Niobium-91 will remain 93.75 g
Further explanation
The atomic nucleus can experience decay into 2 particles or more due to the instability of its atomic nucleus.
Usually radioactive elements have an unstable atomic nucleus.
The main particles are emitted by radioactive elements so that they generally decay are alpha (α), beta (β) and gamma (γ) particles
General formulas used in decay:
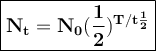
T = duration of decay
t 1/2 = half-life
N₀ = the number of initial radioactive atoms
Nt = the number of radioactive atoms left after decaying during T time
Half life -t1/2 of Niobium-91 =680 years
T=duration time=2040 years
No=initial sample=750 g
Niobium-91 will remain :