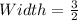Answer:

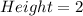 and
and
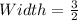
Step-by-step explanation:
Given
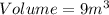
Represent the height as h, the length as l and the width as w.
From the question:

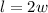
Volume of a box is calculated as:

This gives:

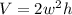
Substitute 9 for V
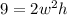
Make h the subject:
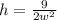
The surface area is calculated as:
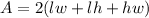
Recall that:
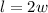
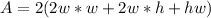
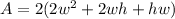

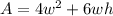
Recall that:
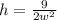
So:
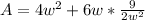
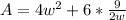
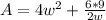
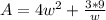
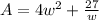
To minimize the surface area, we have to differentiate with respect to w
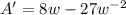
Set A' to 0
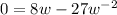
Add
 to both sides
to both sides
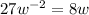
Multiply both sides by
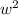
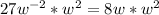
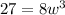
Make
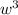 the subject
the subject
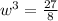
Solve for w
![w = \sqrt[3]{(27)/(8)}](https://img.qammunity.org/2021/formulas/engineering/college/jvi5b13s4sr6l69tlfpy8b7loqj2t6znti.png)
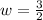
Recall that :
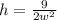 and
and
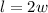
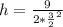
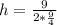
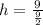
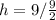
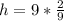

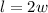
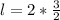
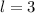
Hence, the dimension that minimizes the surface area is:

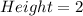 and
and