Answer:
(a) A = (20mg)/(2^(t/30))
(b) 12.6mg
(c) 129.6years
Explanation:
To calculate the amount remaining after a number of half-lives, n, we can make use of:
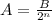
Where A = amount remaining
B = initial amount
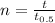
(a) A = (20mg)/(2^(t/30))
(b) Mass after 20years
A = (20mg)/(2^(20/30)) ≈ 12.6mg
(c) After how long will only 1mg remain:
1mg = (20mg)/(2^(t/30))
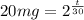
Taking log of both sides we have:
Log(20) = (t/30)log(2)
t/30 = (log(20))/(log(2)) ≈ 4.3
t/30 = 4.3
t = 30 x 4.3 ≈ 129.6years.